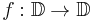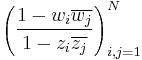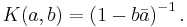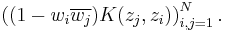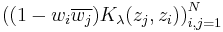Nevanlinna–Pick interpolation

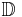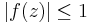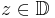In complex analysis, Nevanlinna–Pick interpolation is the problem of finding a holomorphic function from the unit disc to the unit disc (denoted $\mathbb{D}$ ), which takes specified points to specified points. Equivalently, it is the problem of finding a holomorphic function f which interpolates a data set, subject to the upper bound $\left\vert f(z) \right\vert \le 1$ for all $z \in \mathbb{D}$ .

More formally, if z₁, ..., z_N and w₁, ..., w_N are collections of points in the unit disc, the Nevanlinna–Pick problem is the problem of finding a holomorphic function

$f:\mathbb{D}\to\mathbb{D}$

such that

f(w_i) = z_i for all i between 1 and N.

The problem was independently solved by G. Pick and R. Nevanlinna in 1916 and 1919 respectively. It was shown that such an f exists if and only if the Pick matrix

$\left( \frac{1-w_i \overline{w_j}}{1-z_i \overline{z_j}} \right)_{i,j=1}^N$

is positive semi-definite. Also, the function f is unique if and only if the Pick matrix has zero determinant. Pick's original proof was based on Blaschke products.

Generalisation

It can be shown that the Hardy space H² is a reproducing kernel Hilbert space, and that its reproducing kernel (known as the Szegő kernel) is

$K(a,b)=\left(1-b \bar{a} \right)^{-1}.\,$

Because of this, the Pick matrix can be rewritten as

$\left( (1-w_i \overline{w_j}) K(z_j,z_i)\right)_{i,j=1}^N.\,$

This description of the solution has motivated various attempts to generalise Nevanlinna and Pick's result.

The Nevanlinna–Pick problem can be generalised to that of finding a holomorphic function 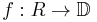$f:R\to\mathbb{D}$ that interpolates a given set of data, where R is now an arbitrary region of the complex plane.

M. B. Abrahamse showed that if the boundary of R consists of finitely many analytic curves (say n + 1), then an interpolating function f exists if and only if

$\left( (1-w_i \overline{w_j}) K_\lambda (z_j,z_i)\right)_{i,j=1}^N\,$

is a positive semi-definite matrix, for all λ in the n-torus. Here, the K_λs are the reproducing kernels corresponding to a particular set of reproducing kernel Hilbert spaces, which are related to the set R. It can also be shown that f is unique if and only if one of the Pick matrices has zero determinant.

References

Agler, Jim; John E. McCarthy (2002). Pick Interpolation and Hilbert Function Spaces. Graduate Studies in Mathematics. AMS. ISBN 0-8218-2898-3.
Abrahamse, M. B. (1979). "The Pick interpolation theorem for finitely connected domains". Michigan Math. J. 26 (2): 195–203. doi:10.1307/mmj/1029002212.